[알고리즘] 복잡성 (Complexity)

1. 시간 복잡도

시간 복잡도는 서로 다른 알고리즘의 효율성을 비교할 때 사용한다. 여러 알고리즘을 비교하는 시간 복잡도에는 몇 가지 규칙이 존재하는데, 내용은 아래와 같다.

1. 입력값(input)은 항상 0보다 크다. (input ≥ 0)

   시간복잡도 에서 n은 입력값을 의미하는데, 항상 양수를 가진다고 가정하기 때문에 시간 복잡도는 항상 0보다 크다.

2. 함수는 많은 입력값이 있을 때 더 많은 작업을 하게 된다.

   많은 요소가 있다면 함수는 더 많은 작업을 하게 된다. 값이 많을수록 하는 일이 적은 함수는 Computer Science에서는 존재할 수 없다.

3. 시간 복잡도에서는 모든 상수를 삭제한다.

   예를 들어 실제 복잡도가 3n 이어도 n이 된다. 3n, 5n, 10n, 100n 모두 복잡도가 n인 알고리즘이다. 알고리즘의 효율을 생각할 때 작은 값은 생각하지 않는다. 값이 매우 큰 경우를 고려하지 작업이 1개, 2개는 알고리즘의 효율을 무시할 정도로 큰 차이가 존재하지 않는다.

4. 낮은 차수의 항은 모두 무시한다.

   알고리즘의 실제 복잡도가 $n^3 + n^2 + n + 50$일 때, 최고 차항을 제외한 차수는 알고리즘의 시간 복잡도에 아무런 영향을 미치지 않는다. 앞서 말했듯, 알고리즘의 효율을 고려하는 경우는 매우 큰 값의 입력을 가정한다. 입력이 매우 크면 최고차항만 고려해야 한다. 따라서 $n^3 + n^2 + n + 50$은 복잡도가 $n^3$이다.

5. 로그에서는 로그의 밑은 무시한다.

   자바에서 Math.log(2)는 자연로그 $ln(2)$를 의미한다. 자연로그 값을 알고 있으면 밑이 다른 로그도 알 수 있다. 자연로그를 분자에 대입하고 바꾸고자 하는 밑의 로그로 나누면 된다. $log_{10}2 = ln(2) / ln(10)$, 모든 로그는 서로 배수 관계이다. 따라서 복잡도에 대해 이야기 할 때 로그의 밑은 고려하지 않아도 된다. 로그 밑은 무시하고 $log\ n$알고리즘이라 표현하면 된다.

6. 등호를 사용해 표현한다.

   Big-Oh 표기법의 의미는 함수의 집합에 속한다는 뜻이다. 2n을 빅 오 표기번으로 표현하면 $O(n)$이고, $2n \in O(n)$을 의미한다. 즉 집합에 포함된다는 뜻이다.

상수 시간에 동작하는 알고리즘의 시간 복잡도는 1 또는 문자 C를 사용해 나타낸다. 한 번의 계산만 하면 되는 경우로 입력값 n과는 독립적인 관계를 가진다.

$log\ n$ 알고리즘은 주로 정렬이나 트리에 많이 등장한다. 로그는 보통 무언가를 반으로 나누거나, 2를 곱할 때 자주 사용된다. 만약 for문을 통해 무언가를 탐색해서 반으로 나누거나 2를 곱하면 밑이 2인 로그가 되고, 10으로 나누거나 곱하면 밑이 10인 로그가 된다. 하지만 시간 복잡도를 표시할 땐 $log\ n$이라 한다.

시간 복잡도가 $n$인 경우 각각의 요소마다 한 번씩 작업을 하는 경우이다. 리스트를 탐색하거나, 연결 리스트를 탐색할 때 복잡도는 $n$이 된다.

시간 복잡도가 $n^2$인 경우 모든 요소를 서로 비교하는 경우가 있다. 굉장히 비효율적인 정렬 알고리즘인, 거품 정렬 알고리즘의 경우 복잡도가 $n^2$이다.

시간 복잡도가 $n!$인 경우는 그래프에서 외판원 문제와 같은 경우가 있다. 외판원 문제는 어떤 사람이 각 도시를 한 번만 방문해 모든 도시를 돌아다니는 최단 경로를 찾는 문제이다. 일반적으로 $n!$의 복잡도를 가진다.

2. Big-Oh(빅 오) 표기법

• Big-Oh(빅 오) 표기법: 알고리즘의 효율성을 표시하는 표기법, 어떤 알고리즘을 다른 알고리즘과 비교해서 표현하는 것이 가능해진다.

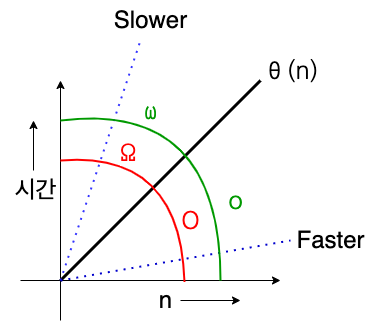
위 그래프는 복잡도가 n인 알고리즘에 Big-Oh 표기법을 적용한 결과이다. x축은 복잡도 n, y축은 시간(필요한 일의 양)이나 메모리를 의미한다.

다른 알고리즘이 이 그래프의 어떤 위치에 있는지에 따라 복잡도 n인 알고리즘과 다른 알고리즘의 복잡도를 비교할 수 있다. $θ(n)$보다 아래에 있다면, 같은 일을 하는 데 시간이 덜 드는 빠른 알고리즘이고, 위에 있다면 더 느린 알고리즘이다.

• O(빅 오 복잡도): 비교 대상인 그래프가 일치 혹은 아래에 있을 때. 비교 대상인 다른 알고리즘과 같거나 더 빠르다. (Same or faster)
  • 알고리즘의 최악의 실행 시간을 표기하는 방법이다. 즉 $O(n)$은 아무리 최악의 상황이라도 이 시간안에 처리할 수 있는 성능을 보장한다는 의미이다.
• θ(세타 복잡도): 비교 대상인 그래프가 일치할 때. 비교 대상인 알고리즘과 똑같다. (Same rate)
  • 알고리즘의 평균 실행시간을 표기하는 방법이다.
• $\Omega$(빅 오메가 복잡도): 비교 대상인 그래프가 일치 혹은 위에 있을 때. 비교 대상인 알고리즘과 같거나 느리다. (Same or slower)
  • 알고리즘의 최상의 실행 시간을 표기하는 방법이다.
• o(리틀 오 복잡도): 비교 대상인 그래프가 아래에 있을 때. 비교 대상인 다른 알고리즘보다 빠르다. (faster)
• $\omega$(리틀 오메가 복잡도): 비교 대상인 그래프가 위에 있을 때. 비교 대상인 다른 알고리즘보다 느리다. (slower)

Big-Oh 표기법의 이해를 위해 몇 가지 문제를 살펴본다.

1. $n^{4/3} = O(n\ logn)$ ?

   False, 위에 사용한 그래프와 같은 형식으로 그리면 O(nlogn)는 같거나 더 빠른 알고리즘 이기 때문에 n^(4/3)은 Same or faster에 포함되지 않는다.

2. $3n^3 + 4n^2 + 5n + 6 = \theta(n^3)$ ?

   True, 위 식을 정리하면 $n^3 = \theta(n^3)$이고, Same rate이다.

3. $n(n-1)/2 = O(n^2)$ ?

   True, 2번 문제와 같이 정리하면, $n^2 = O(n^2)$이고, Same or faster에 포함된다.

4. $2^n = \omega(n)$ ?

   True, 2^n은 n보다 느린 알고리즘 이다.

5. $n^3 = O(n^2)$ ?

   False, n^3은 n^2보다 빠르게 증가한다. 따라서 더 느린 알고리즘이기 때문에 n^2의 Same or faster에 포함되지 않는다.

6. $n^2 = O(n^3)$ ?

   True, n^2이 더 빠른 알고리즘이기 때문에 n^3의 Same or faster에 포함된다.

3. 공간 복잡도

공간 복잡도는 알고리즘이 사용하는 메모리 크기를 의미한다. 과거 메모리가 부족한 상황에서는 공간 복잡도가 매우 큰 비중을 차지했으나, 현재 대용량 시스템이 널리 보급되어 시간 복잡도가 더 우선시 되는 상황이 되었다.

프로그램을 실행 및 완료하는데 필요한 저장공간의 크기를 의미하며 총 필요 저장 공간은 고정 공간과 가변 공간 두 가지로 나뉜다.

• 고정 공간: 변수 및 상수를 저장하는 공간. 즉, 코드를 저장하는 공간
• 가변 공간: 실행 중 동적으로 필요한 공간.

$S(P) = c + S_{p}(n)$, c는 고정 공간이고 $S_{p}(n)$은 가변 공간이다. 고정 공간은 상수값 이기 때문에, 가변 공간에 의해 공간 복잡도는 결정된다.

참고 URL

네이버 부스트 코스: 자바로 구현하고 배우는 자료구조