9 분 소요

Reference

자바로 구현하고 배우는 자료구조


1. What’s Hash?

  • 연결 리스트(LinkedList)는 유용한 점이 많은 자료구조
    • 수용량이 정해져 있지 않아 메모리의 허용치 내에서 크기에 관한 고민을 하지 않아도 됨 → 반면 배열(Array)은 고정된 크기를 가짐
    • 상수 시간 O(1)로 데이터를 추가 하거나 제거할 수 있음
    • 스택과 큐를 구현하기에 알맞은 자료구조
      • 배열과 달리 수용량이 정해져 있지 않아 값을 추가하는데 크기 관련 문제가 발생하지 않음
    • 하지만, 어떤 값을 탐색할 때 O(N)의 시간 복잡도를 가짐(모든 요소를 확인해야 함)

해시 자료구조

  • 해시(Hash): 데이터를 빠르게 추가하거나 제거하도록 만든 데이터 구조
    • 연결 리스트의 단점은 리스트에서 무언가를 찾고 싶을 때 무조건 모든 요소를 살펴봐야 한다는 것 O(N). 이러한 단점을 해결한 자료구조가 해시
    • Key, 그리고 그와 연관된 Value를 가지고 있는 자료구조
    • Key가 주어지면 바로 그와 연관된 Value를 찾을 수 있음, O(1)
      • value = hash.get(key)
  • 수업을 수강하는 학생의 ID 와 점수가 있다고 가정
    • StudentId = key
    • Grade = value
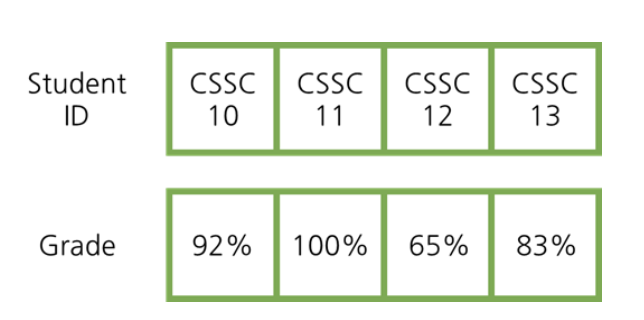
CSSC010 -> 92
CSSC011 -> 100
CSSC012 -> 65
CSSC013 -> 83
  • 해시 함수(Hash Function): hashCode()메서드를 작성
public class Main {

	static int hashCode(String id) {
		return Integer.parseInt(id.replaceAll("CSSC", ""));
	}

	public static void main(String[] args) {
		String[] studentId = {"CSSC010", "CSSC011", "CSSC012", "CSSC013"};

		for (String id : studentId) {
			// CSSC 를 제거해 번호만 남긴뒤 정수형으로 변환
			System.out.println("id = " + id + ", key = " + hashCode(id));
		}
	}

}

해시 자료 구조의 메서드

  • add(): 특정 값을 추가
  • remove(): 특정 값을 제거
  • find() / lookup(): 특정 값을 탐색
  • change(): 특정 요소를 수정
  • allEntries(): 자료 구조에 있는 모든 키와 값들을 꺼내기, $\theta(N)$.
  • allKeys(): 자료 구조에 있는 모든 키를 꺼내기, $\theta(N)$.
  • allValues(): 자료 구조에 있는 모든 값을 꺼내기, $\theta(N)$.
  • size(): 자료 구조의 크기, O(1)
  • isEmpty(): 자료 구조가 비어있는지 확인, O(1)
  • isFull(): 자료 구조가 가득 차 있는지 확인, O(1)
  • loadFactor(): (키의 개수 / 자료 구조의 크기), 적재율로 1 보다 큰 경우 충돌(Collision) 문제가 발생할 수 있음, O(1)


2. 해시 함수(Hash Function)

  • 가장 중요한 것은 데이터의 속성(property)
  • 해시 함수는 빠르게 계산되어야 함
    • 수 많은 데이터를 처리하기 위해 무엇이 주어지든 빨리 계산되게 구현
  • 중복된 요소(equal)가 있으면 같은 값을 돌려줘야 한다
    • if two things are “equal” should return the same value
  • 항상 같은 값을 반환해야 한다
    • 동일한 실행상황일 때 어떤 값의 해시 함수 결과는 항상 같아야 한다. 즉, A가 2번 입력되었을 때 동일한 값이 나와야 한다.
  • 코드를 새로 실행하면 객체가 같더라도 다른 값이 나올 수 있다.
    • 만약 DB 같은 저장공간에 값을 저장하는 상황이라면 위 조건은 만족하지 않게 구현해야 한다.
    • Object 클래스의 toString, equals, hashCode와 같은 메소드들은 오버라이딩을 하지 않으면, 기본적으로 메모리 위치를 기반으로 코드가 실행. 객체는 코드가 새로 실행될 때마다 메모리 상의 다른 위치에 할당되기 때문에 오버라이딩 하지 않으면, 입력으로 들어온 객체가 같더라도 새로 실행 시 다른 값을 리턴하게 된다.
  • 코드에서 최대한 충돌이 일어나지 않도록 구현 해야 한다.


3. 해시 충돌(Hash Collision)

  • 해시 충돌(Hash Collision): 서로 다른 값을 가진 키가 일치하는 경우 발생하는 문제
  • 전화번호 데이터를 저장하기 위한 배열이 있을 때, 전화번호를 key 로 설정하고 이름을 value 로 설정한다.
    • 전화번호는 문자열이기 때문에 변환하기 위해 -를 기준으로 값을 나누어 더하는 hashCode()를 이용해 변환 후 key로 설정할 때 문제가 발생 → 전화번호가 다른데 해시 함수의 반환 값이 같게 된다. 이를 해시 충돌이라 한다.


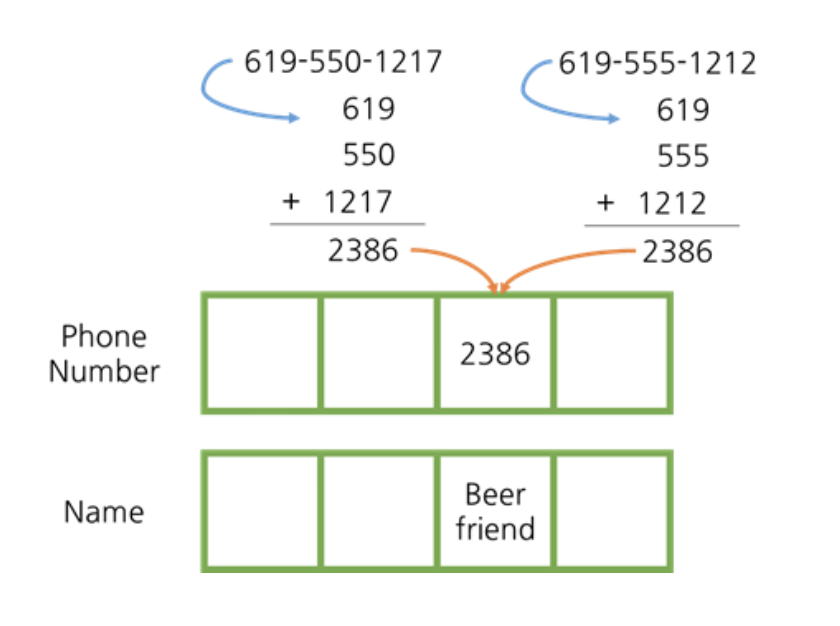
4. 해시 함수에서 문자열

String s = "my name is Rob";
char c = s.charAt(6);
// c = 'e'

int i = s.charAt(6); // charAt()에 유니코드로 변경되도록 오버라이딩 되어있음
System.out.println(i); // 컴파일 됨, 유니코드 값이 출력: 101
  • 유니코드
'0' ~ '9': 48 ~ 57
'A' ~ 'Z': 65 ~ 90
'a' ~ 'z': 97 ~ 122

문자열을 위한 hashCode()

  • "this": 116 + 104 + 105 + 115 = 440
  • "hits": 104 + 105 + 116 + 115 = 440
  • 단순히 유니코드 값을 더하는 해시 함수는 좋은 구현이 아님 → 충돌 문제 발생
  • 문자의 위치에 따라 상수 g를 곱하는 횟수를 다르게 해서 충돌 문제를 해결
  • this 를 변환하는 식 = 116 + g(104 + g(105 + g(115)))
    • 115
    • g(115)+ 105
    • g*g(115) + g(105) + 104
    • g*g*g(115) + g*g(105) + g(104) + 116
    • = $g^0(116) + g^1(104) + g^2(105) + g^3(115)$
public int hashCode(String s) { // this

  int g = 31;
  int hash = 0;

  for(int i = s.length() -1; i >= 0; i--) {
    hash = g * hash + s.charAt(i);
  }

  return hash;
}


5. 해시 크기 최적화

public int hashCode(String s) {...}

// 자바
// -10 % 3 = -1
  • 해시 함수가 문자열을 파라미터로 받고 정수를 반환해 줄 때, 이 값을 배열의 인덱스로 사용하기 위해서는 최적화가 필요
    • 충돌을 방지해 줘야 함
  • 해시 충돌을 방지하기 위해 해시 크기를 최적화 해줘야 한다.
    • 해시의 크기를 홀수로 설정하여 %연산자를 사용했을 때 다양한 결과가 나오게
      • 짝수는 최소 공약수 2를 공유하기 때문에 사용하면 충돌이 많이 일어난다. 반면 홀수는 최소공약수를 공유하지 않기 때문에 좀 더 균등하게 값이 들어갈 가능성이 높아 충돌을 방지할 수 있다.
    • 해시의 크기를 소수로 설정하여 %연산자를 사용했을 때 다양한 결과가 나오게
      • 상대적으로 값이 균등하게 들어간다, 소수는 1과 자기 자신을 제외한 수의 배수가 될 수없기 때문이다. 배수가 나오는 경우의 수를 최대한 줄이면 최대한 충돌을 방지할 수 있다.
    • 해시의 크기 자체를 늘리기
      • %연산을 사용하면 해시 크기 - 1 만큼 나머지가 나오기 때문에 경우의 수가 많다
      • 자바의 해시 함수 크기는 31로 설정되어 있음 (마르센 소수 2^n - 1 꼴의 소수, 시프트 연산을 이용해 빨리 계산하기 위해)


6. 해시 값을 양수로 설정하기

보수

  • 자바는 2의 보수를 사용: 첫 숫자가 부호를 결정
    • 0: 양수
    • 1: 음수
(2진수) 
0000 0000 = 0
0000 0001 = 1
0000 0010 = 2
...
0111 1110 = 126
0111 1111 = 127

1111 1111 = -1
1111 1110 = -2
...
1000 0010 = -126
1000 0001 = -127
1000 0000
  • 음수를 변환하기 위해 data.hashCode()값과 0x7FFFFFFF를 & 연산해 준다
    • 0x7FFFFFFF: “0111 1111 1111 1111 1111 1111 1111 1111”
      • 0111 = 7
      • 1111 = F
return data.hashCode() & 0x7FFFFFFF;
  • -1 & 0x7FFFFFFF = 2,147,483,647 ($2^{63} - 1$)
  • -10 & 0x7FFFFFFF = 2,147,483,638 ($2^{63} - 10$)

hashCode 값을 테이블에 맞는 인덱스로 변경하기

  • data를 배열의 어느 위치에 넣을 것인지 결정
int hashVal = data.hashCode(s);
hashVal = hashVal & 0x7FFFFFFF; // 해시값을 양수로 변경 (이미 양수인 경우 그대로)
hashVal = hashVal % tableSize; // 양수로 변경한 해시값 % 테이블 크기


7. LoadFactor 메서드

  • LoadFactor: 테이블에 데이터가 얼만큼 있는지 알려줌
    • ex: 배열이 있고 여러 개의 요소를 추가할 때 배열의 크기에 비해 비교적 얼만큼 찼는지 표현
  • $\lambda$ (적재율) = Number of Entries (현재 자료구조에 있는 요소 수) / 자료 구조의 크기
    • $\lambda$ = 0, 자료 구조가 비어있다는 의미
    • $\lambda$ = 0.5, 자료 구조가 절반 차있다는 의미
    • $\lambda$ = 1, 자료 구조가 가득 차있다는 의미 → 문제 발생(충돌)
int[] arr = new int[100];
for (int i = 0; i < 20; i++) {
  arr[i] = i;
}

// arr의 적재율 = 20 / 100 = 0.2


8. 해시 충돌(Collision)을 해결하는 방법

  • 배열에 넣고 싶은 객체 x가 있다고 가정
    • 객체 x의 hashCode()는 정수를 반환
Something[] arr = new Something[10];
int tableSize = arr.length;

int h = x.hashCode();
h = h & 0x7FFFFFFF; // 해시값을 양수로 변경 (이미 양수인 경우 그대로)
h = h % tableSize; // 양수로 변경한 해시값 % 테이블 크기

arr[h] = x;

// 새로운 객체 y가 주어지면
h = y.hashCode();
h = h & 0x7FFFFFFF;
h = h % tableSize;
  • 만약 y의 h 계산값이 x의 계산값과 같으면 충돌이 일어나게 됨
    • 해결방법은? 다음 공간에 배정, arr[h + 1] = y
    • y를 찾으려할 때 계산한 h에 없다면 뒤를(다음 칸) 계속 확인 → 선형 조사법

선형 조사법(Linear Probing)

  • 채우려는 공간이 이미 차 있다면, 비어있는 칸을 찾을 때까지 다음 칸을 확인하는 방법
    • 비어있는 칸을 찾아 그 곳에 채운 후 위치가 바뀌었다는 사실을 알려야 함
    • 해시값을 증가시켜 해시 충돌을 피하는 기법
  • 만약 중간에 있는 객체를 제거하는 상황에서 제거한 후 null 로 채운다면?
    • 문제 발생: 선형 조사법은 앞에서 부터 빈 공간이 있을 때까지 다음 칸을 확인하는 방법인데 중간에 null을 발견하면 해당 객체가 삭제한 공간 뒤에 존재해도 존재하지 않는 객체라 판단함
    • 해결 방법: flag를 이용해 표시해줘야 함. 삭제 후 null값을 넣고 flag를 이용해서 원래 값이 있던 공간임을 표시
  • 데이터가 순차적으로 나열되어 자료의 크기가 커질수록 비효율적인 조사법이 됨
    • 이 문제를 해결하기 위해 2차식 조사법(Quadratic Probing)이 고안
  • 적재율이 증가하면서 0.6일 때즘 자료구조의 크기를 늘리는 것이 좋음

2차식 조사법(Quadratic Probing)

  • 채우려는 공간이 이미 차 있다면, 다음 칸 대신 1부터 순서대로 제곱하여 더한 칸을 확인하는 방법
    • hashValue + ($1^2, 2^2, 3^2,\ …\ n^2$)
    • 테이블의 크기를 넘어가면 % 연산을 통해 테이블 크기의 범위 내로 줄임
    • 해시값을 증가시켜 해시 충돌을 피하는 기법
  • 적재율이 증가하면서 0.6일 때즘 자료구조의 크기를 늘리는 것이 좋음

이중 해싱(Double Hashing)

  • hasCode()를 2개 정의해 채우려는 공간이 이미 차있으면 두 hashCode()결과값을 더해 테이블 내의 위치를 표현하는 방법
    • 두 번째 hashCode()는 첫 번째 함수와 달라야 함
    • 두 번째 hashCode()는 0을 반환하면 안됨
    • 선형, 2차식 조사법에 비해 다른 해시 함수를 사용해 데이터를 더 골고루 넣을 수 있음
    • 하지만 두 개의 해시 함수를 정의해야 함 → 로직이 복잡해짐
    • 자바에서는 두 개의 해시 함수가 있는 것을 보장하지 않음


9. 체이닝 (Chaining)

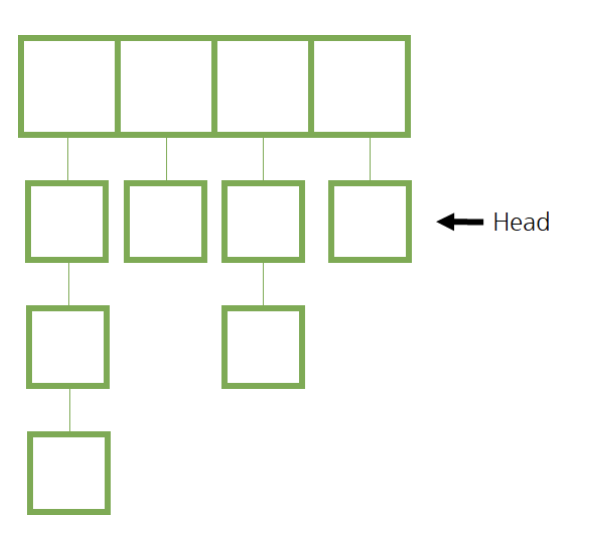
  • 체이닝(Chaining): 요소마다 연결 리스트를 만들어 수많은 데이터를 수용할 수 있게 하는 방법, 해시 충돌을 피할 수 있음
    • 해시는 사실상 배열 한 개로 구성되어 있음
    • 그 배열에 요소를 추가하는 구조
    • 배열의 위치마다 새로운 자료 구조를 만들면서 수많은 데이터를 수용할 수 있도록 만드는 것
    • 그 새로운 자료구조는 연결 리스트(Linked List)를 이용
    • 각 배열의 위치마다 head가 존재
    • 체인 해시는 가장 안정적이고 보편적으로 사용되는 최고의 자료 구조
    • 각 배열의 위치마다 head가 존재
int h = a.hashCode();
h = h & 0x7FFFFFFF;
h = h % tableSize;

arr[h].add(a);

h = b.hashCode();
h = h & 0x7FFFFFFF;
h = h % tableSize;

arr[h].add(b);

  • 이미arr[h] 에 요소가 있다면? arr[h]는 연결 리스트이기 때문에 add를 이용해 객체를 추가해도 연결 리스트에 추가됨 → 상수 시간 O(1)로 어떤 요소든 추가하고 제거하고 찾을 수 있음, 또 수용할 수 있는 요소 개수에 제한도 없어짐

    • 추가하려는 객체의 수가 tableSize 보다 많아도 연결 리스트를 키우면 되니 크기에 관한 고민이 줄어듦
    • 즉, 수용 가능한 요소 개수에 제한이 없어지고 크기 조정도 자주 할 필요가 없어짐

  • 체인 해시의 적재율은?

    • $\lambda$(적재율) = 항목의 개수(Numberm of Entries) / 가능한 체인 개수(연결 리스트의 개수)
    • 적재율이 1이 넘어가도 객체를 추가하는데 큰 문제가 없어짐

체인 해시의 문제점

  • 하나의 체인이 너무 길어지면 결국 연결 리스트와 시간 복잡도가 같아지는 문제가 발생
    • 하나의 체인에 값이 계속해서 추가될 경우 어떤 객체를 찾으려 할 때 O(N) 시간이 걸릴 수 있음
  • 효율적인 체인 해시 사용을 위해 hashCode()가 다양한 값을 반환할 수 있도록 구현해야 함
    • 다양한 체인에 객체를 저장하면 상수 시간 O(1)로 추가, 삭제를 할 수 있음


10. 재해싱(Rehashing)

  • 체인 해시는 배열의 크기보다 더 많은 요소를 담을 수 있는 구조

    • 적재율이 1이 되도 데이터가 없는 배열 공간이 있음
    • 하지만 연결 리스트에 값이 많아지면 탐색에 O(N)의 시간이 걸리는 단점이 있음

  • 기존 배열은 적재율이 1에 가까워지면 크기를 2배로 늘려 0번 부터 차례대로 인덱스를 유지하며 새로운 배열에 기존 값을 복사하는 방법으로 적재율을 줄였음

  • 체인 해시는 배열의 크기를 두 배로 늘려 인덱스를 그대로 복사하는 방법이 아닌 재해싱을 통해 새로운 배열에 값을 재분배

    • 크기가 2배인 배열을 만듦
    • 아래 코드를 통해 새로운 배열에 재분배
    int h = a.hashCode();
h = h & 0x7FFFFFFF;
h = h % newTableSize; // 기존 배열 크기의 2배

  • 왜 인덱스를 유지해서 새로운 배열로 옮기면 안되나? 처음 값을 저장할 때도 아래 코드를 사용했었는데 tableSize를 2배로 늘린 시점에서 인덱스를 그대로 유지해서 저장하면 제거나 탐색을 할 때 문제가 발생. 즉, 값을 저장할 때 tableSize를 10 사용했었는데 크기를 늘리고 제거나 탐색을 할 때 새로운 tableSize인 20을 사용하기 때문에 결과값이 다름.

    • h 값이 11이 나와 % 연산을 통해 1번 인덱스에 저장했는데 크기를 2배로 늘린 후에는 % 연산을 통해 11번 값이 나와 탐색이나 제거할 때 존재하지 않는 객체라는 판단이 될 수 있음
    int h = a.hashCode();
h = h & 0x7FFFFFFF;
h = h % tableSize;


11. 해시 클래스 구현


댓글남기기

참고

[프로그래밍] 좋은 테스트 코드 작성하기

6 분 소요

References Testing, Oh my! 스프링 캠프 2019: 무엇을 테스트할 것인가? 어떻게 테스트할 것인가? [번역글] UnitTest By Martin Fowler 3월 우아한테크세미나: 우아한 ATDD

[자바] final 키워드 & 불변 객체

2 분 소요

References [10분 테코톡]시카의 Java final과 불변 객체) 불변 객체(Immutable Object) 및 final을 사용해야 하는 이유 - Mangkyu님 블로그

[자바] Java Enum

2 분 소요

References Java Enum 활용기 - 우아한 기술 블로그