[자료구조] 자바(Java) 트리(Tree)

2023-04-11 11 분 소요

Reference

자바로 구현하고 배우는 자료구조

📌 What’s Tree?

트리: Node와 Edge를 이용해 사이클을 이루지 않도록 구성한 데이터 구조
어디에 사용 되나?
- 트리 중 이진 트리(binary tree)형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용
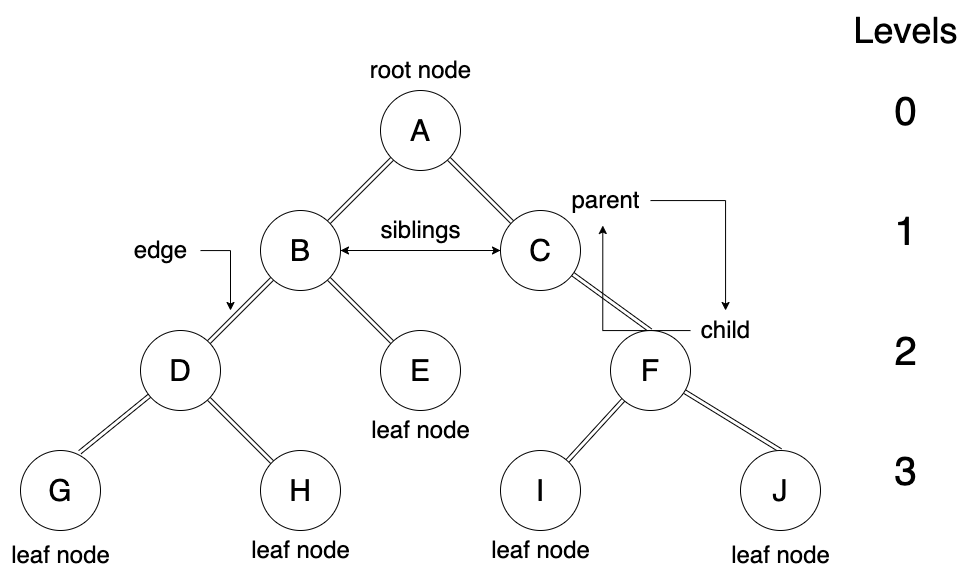
Node: 트리에서 데이터를 저장하는 기본 요소
Root Node: 트리 맨 위에 있는 노드
Level: 최상위 노드를 Level 0 으로 하였을 때, 하위 Edge로 연결된 노드의 깊이를 나타냄
Parent Node(부모 노드): 어떤 노드의 이전(-1) 레벨에 연결된 노드
Child Node(자식 노드): 어떤 노드의 다음(+1) 레벨에 연결된 노드
Leaf Node(Terminal Node): 자식 노드가 하나도 없는 노드
Sibling(Brother Node): 동일한 부모 노드를 가진 노드
Depth: 트리에서 노드가 가질 수 있는 최대 Level
Edge(Branch, 간선): 노드와 노드드를 연결하는 선

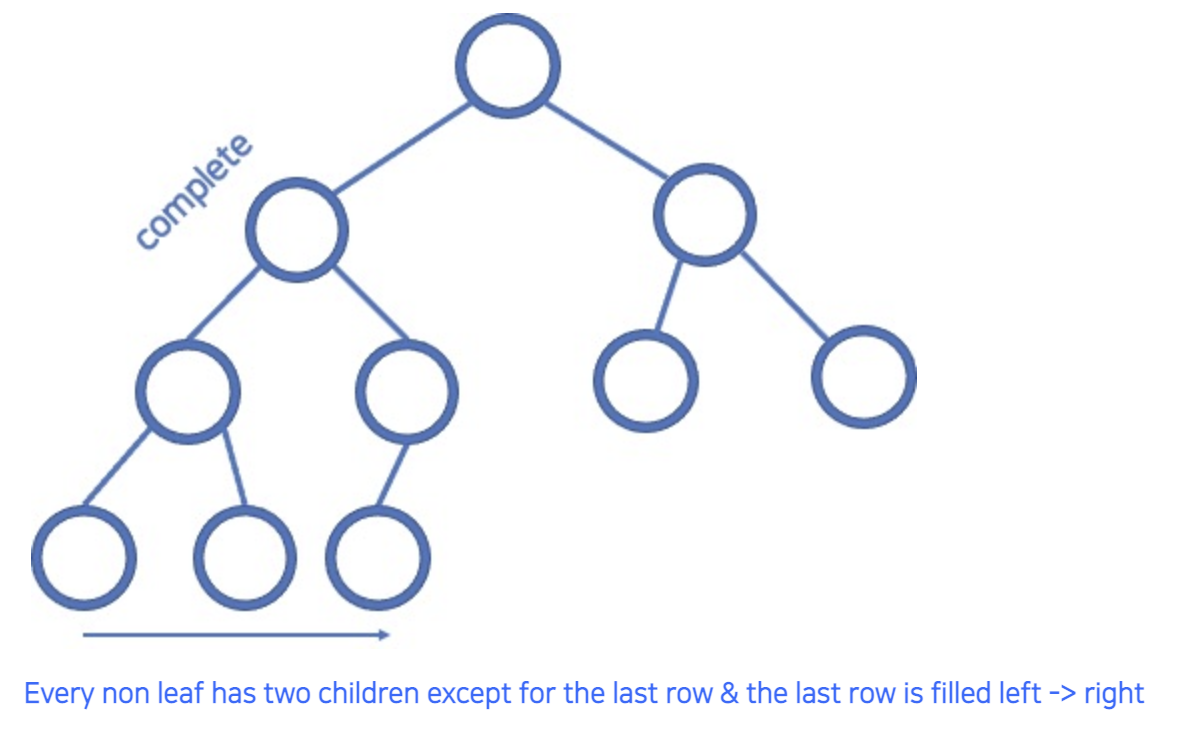
완전 트리(Complete tree): 모든 잎이 아닌 노드(Non-leaf node)가 2개의 자식 노드를 가지고 있고 마지막 줄(Last level)은 왼쪽에서 오른쪽 순서로 채워져 있는 트리
- leaf node의 레벨이 서로 다를 수 있음

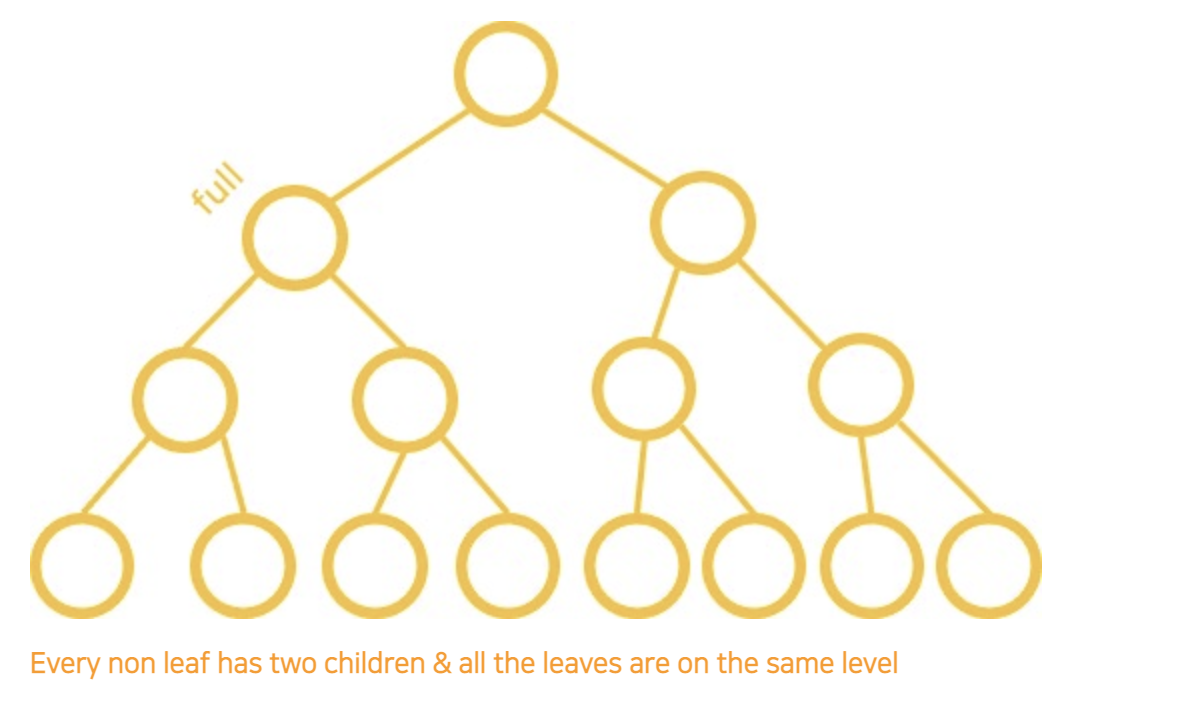
정 트리(Full tree): 모든 잎이 아닌 노드(Non-leaf node)가 2개의 자식 노드를 가지고 있고 모든 leaf node가 같은 레벨에 있는 트리
- leaf node의 레벨이 모두 같음

📌 트리 순회(Trees Traversal)

전위 순회(Pre-order traversal): 루트노드에서 시작하여 왼쪽 자식 노드에 갔다가 오른쪽 자식 노드로 가는 순회 방법
- 다른 모든 노드를 방문하기 전에 루트를 먼저 방문
- 루트 노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드
- A -> B -> D -> G -> H -> E -> C -> F -> I -> J
중위 순회(In-order traversal): 왼쪽 자식 노드에서 시작하여 루트 노드에 갔다가 오른쪽 자식 노드로 가는 순회 방법
- 왼쪽 자식 노드 -> 루트 노드 -> 오른쪽 자식 노드
- G -> D -> H -> B -> E -> A -> C -> I -> F -> J
후위 순회(Post-order traversal): 왼쪽 자식 노드에서 시작하여 오른쪽 자식 노드에 갔다가 루트 노드로 가는 순회 방법
- 왼쪽 자식 노드 -> 오른쪽 자식 노드 -> 루트 노드
- G -> H -> D -> E -> B -> I -> J -> F -> C -> A
너비 우선 순회(Breadth first / Level order traversal): 가장 위에 있는 노드에서 시작하여 왼쪽에서 오른쪽으로 가는 순회 방법
- A -> B -> C -> D -> E -> F -> G -> H -> I -> J
트리의 순회는 보통 재귀(Recursion) 방식을 사용해 구현된다.

📌 트리 표현(Expression trees)

중위 표기식(In-order expression): 중위 순회를 표현, 피연산자 사이 연산자가 있는 구조
- 장점: 익숙한 연산 표현식
- 단점: 괄호와 연산자 우선순위를 고려해야 함. 즉, 왼쪽부터 차례대로 계산할 수 없음
후위 표기식(Post-order expression: 후위 순회를 표현, 피연산자를 표현한 후 연산자가 있는 구조
- 장점: 괄호 필요 없이 수식을 왼쪽부터 차례대로 계산하면 됨. 즉, 연산자의 우선순위를 생각하지 않아도 됨(컴퓨터가 연산하기 더 편한 방법)
- 단점: 익숙하지 않은 표현식

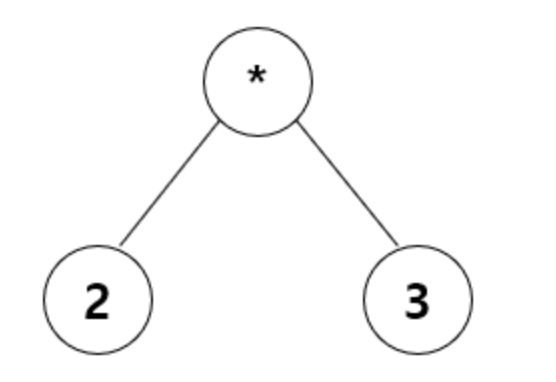
중위 표기식: 2 * 3
후위 표기식: 2 3 *

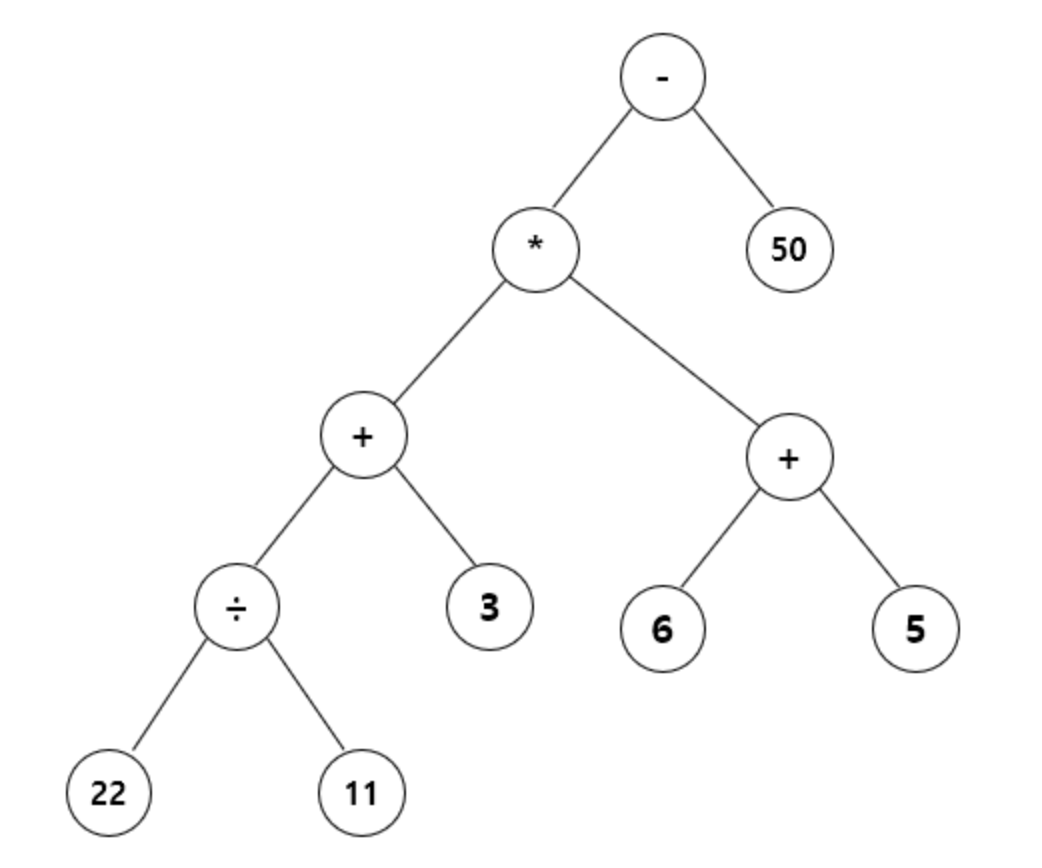
중위 표기식: (((22 / 11) + 3) * (6 + 5)) - 50
후위 표기식: 22 11 / 3 + 6 5 + * 50 -

📌 Node: 데이터를 저장하는 요소

트리에서 지켜야하는 규칙은 작은 데이터가 왼쪽에 위치해야 한다.
- 부모 노드보다 작은 데이터가 왼쪽 자식 노드에 와야 하고 부모 노드보다 큰 데이터가 오른쪽 자식 노드에 와야 한다.

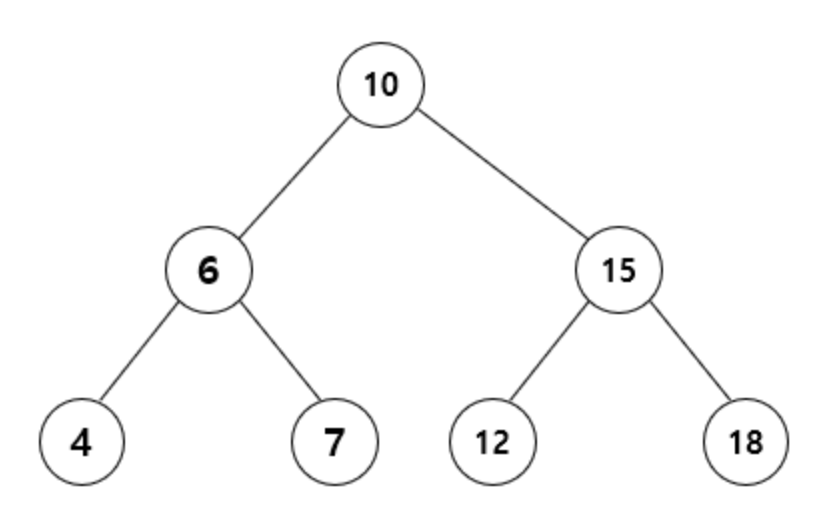
연결 리스트와 비슷하게 트리의 노드는 2개의 포인터와 값이 존재한다.
- 자신의 부모를 가리키는 포인터 parent도 필요할 수 있지만 같은 노드를 최대 3개의 포인터(부모의 포인터 1개, 왼쪽 오른쪽 각 1개)가 가리키게 되어 구현이 복잡해져 생략.
- left: 자신의 왼쪽을 가리키는 포인터
- right: 자신의 오른쪽을 가리키는 포인터

class Node<E> {
	E data; // 저장할 데이터
	Node<E> left; // 왼쪽 자식을 가리키는 포인터
	Node<E> right; // 오른쪽 자식을 가리키는 포인터

	public Node(E obj) {
		this.data = obj;
		left = right = null;
	}
}

📌 트리의 데이터 추가: by Recursion

트리에 새로운 데이터를 추가하는 과정은 아래와 같다.

root node에서 부터 시작
트리의 규칙에 따라 내려간다(부모 보다 작으면 왼쪽, 크면 오른쪽)
null인 부분을 찾으면 그 곳에 새로운 노드를 추가

트리에서 데이터를 추가할 때는 항상 맨 아래에 추가한다.

		/**
		 * @param obj, 추가할 데이터
		 * @param node, 비교할 노드(root 부터 시작)
		 */
		private void add(E obj, Node<E> node) {
			// 추가할 데이터가 현재 노드의 값보다 크면
			if (((Comparable<E>)obj).compareTo(node.data) > 0) {
				// 오른쪽으로 내려가야 한다.
				if (node.right == null) { // 오른쪽이 비어있으면 추가
					node.right = new Node<E>(obj);
					return;
				}

				add(obj, node.right);
			}
			// 추가할 데이터가 현재 노드의 값보다 작거나 같으면
			// 왼쪽으로 내려가야 한다.
			if (node.left == null) {
				node.left = new Node<E>(obj);
				return;
			}

			add(obj, node.left);
		}

		/**
		 * @param obj, 추가할 데이터
		 */
		public void add(E obj) {
			if (root == null) {
				root = new Node<>(obj);
			} else {
				add(obj, root);
			}
			currentSize++; // 트리의 현재 크기++
		}

📌 트리: Contains

트리에 특정 요소가 포함되어있는지 확인하는 과정은 트리에 데이터를 추가하는 과정과 비슷하게 동작한다.

root node에서 시작
트리의 규칙에 따라 내려간다(부모 보다 작으면 왼쪽, 크면 오른쪽)
그 요소를 찾으면 true를 반환하고 null인 노드에 다다르면 false를 반환한다.
1. null인 노드는 leaf node의 포인터가 가리키는 곳. 즉, 끝에 도달했는데 찾으려는 값이 존재하지 않는다는 의미
2. null인 노드는 비어있는 트리의 root node. 즉, 비어있는 트리에는 찾으려는 값이 존재하지 않는다는 의미

	private boolean contains(E obj, Node<E> node) {
		// null인 노드(leaf node의 포인터 or 비어있는 트리의 root)에 도달하면 false
		if (node == null) {
			return false;
		}

		if (((Comparable<E>)obj).compareTo(node.data) == 0) {
			return true;
		}

		if (((Comparable<E>)obj).compareTo(node.data) > 0) { // 찾으려는 값이 현재 노드보다 크면
			return contains(obj, node.right); // 오른쪽으로 이동
		} else { // 찾으려는 값이 현재 노드보다 작으면
			return contains(obj, node.left); // 왼쪽으로 이동
		}
	}

	public boolean contains(E obj) {
		return contains(obj, root);
	}

📌 트리의 데이터 제거

이진 트리에서는 힙처럼 가장 위에 있는 요소를 꺼내서 제거할 수 없다. 트리에서는 규칙을 이용해 특정 요소를 찾아 제거한다.

트리에서 특정한 요소를 제거하는 CASE는 총 3가지가 존재한다.

leaf node를 제거하는 경우
자식이 1개인 노드를 제거하는 경우
자식이 2개인 노드를 제거하는 경우

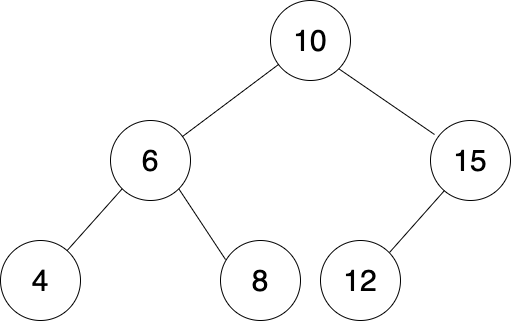
1. leaf node 제거

부모 노드의 포인터를 null로 변경한다.

root node인 10은 left = 6, right = 15를 가리키고 있고, 15는 left = 12, right = null을 가리키고 있고 12는 left와 right가 null을 가리키는 leaf node 이다.
여기서 15의 left를 null로 변경하면 12는 Java GC(Garbage Collector)에 의해 수거된다.

2. 자식이 1개인 노드를 제거

부모 노드의 포인터를 제거하려고 하는 노드의 자식을 가리키게 한다.

15의 부모는 root node인 10이고, 자식은 12이다.
부모인 12의 right 포인터가 12를 가리키도록 변경하면 15는 GC에 의해 수거된다.

3. 자식이 2개인 노드를 제거

중위 후속자와 중위 선임자 중 하나와 자리를 바꾼 후 해당 leaf node를 제거한다.

중위 후속자와 중위 선임자는 leaf node이기 때문에 자리를 바꾸면 leaf node를 제거하는 경우와 똑같다.

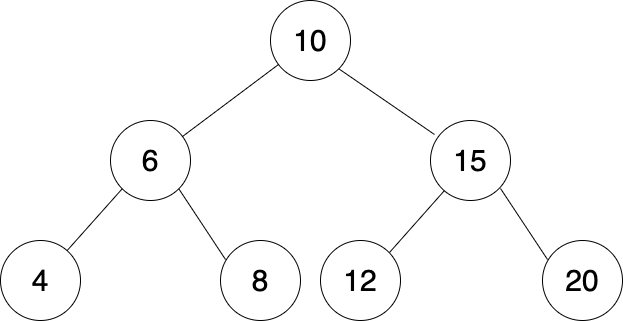
중위 후속자(In-order successor): 주어진 노드의 바로 다음에 큰 값을 갖는 노드
- 제거하고자 하는 노드에서 시작하여 오른쪽으로 한 번 내려갔다가 계속 왼쪽으로 내려간 곳의 leaf node. 중위 선임자는 제거하고자 하는 노드보다 큰 노드들 중에서 가장 작은 노드
- 위 트리에서는 12가 중위 후속자이다.
- 중위 순회 방식으로 노드를 탐색할 때 루트 노드를 방문한 후 만나게 되는 노드이기 때문에 중위 후속자라고 불림
중위 선임자(In-order predecessor): 주어진 노드의 바로 이전에 작은 값을 갖는 노드
- 제거하고자 하는 노드에서 시작하여 왼쪽으로 한 번 내려갔다가 계속 오른쪽으로 내려간 곳의 leaf node. 중위 후속자는 제거하고자 하는 노드보다 작은 노드들 중에서 가장 큰 노드
- 위 트리에서는 8이 중위 선임자이다.
- 중위 순회 방식으로 노드를 탐색할 때 루트 노드를 방문하기 직전에 만나게 되는 노드이기 때문에 중위 선임자라고 불림

📌 트리: 회전

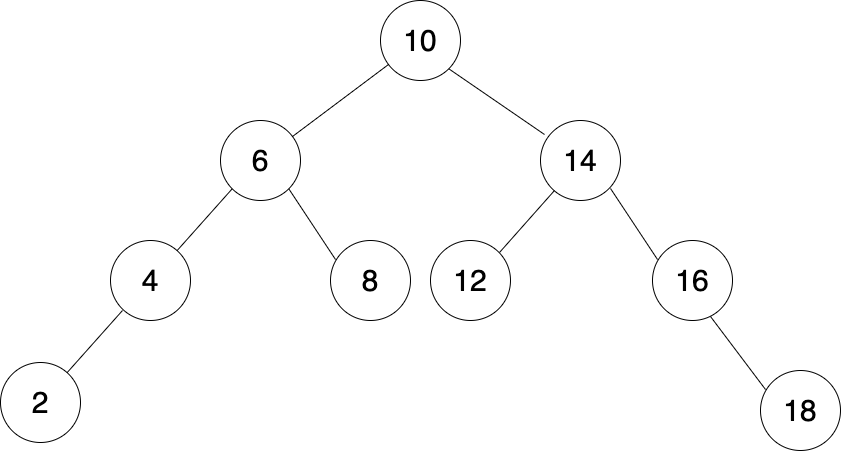
위 그림의 이진 트리는 균형이 잘 잡힌 트리이다. 하지만 항상 트리가 균형이 잘 잡혀있지는 않다. 위 트리가 2를 root node로 하고 오른쪽 자식만 존재하고 모든 왼쪽 노드는 null인 연결 리스트 형태를 갖고 있을 수 있다.

균형 잡혀 있지 않은 트리: 연결 리스트처럼 한 방향으로 나열된 트리

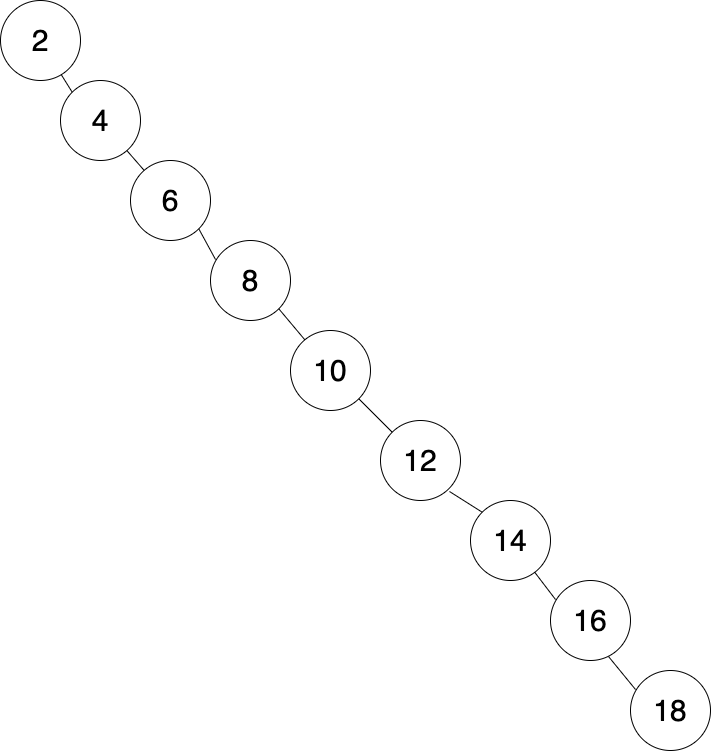
균형 잡힌 트리와 아닌 트리는 탐색의 시간 차이가 존재한다.
- 균형 잡힌 트리: $O(log \ N)$
- 균형이 잡혀 있지 않은 트리: $O(N)$

균형 잡힌 트리를 만들기 위해서는 숫자를 잘 선택해야 하거나 트리를 회전 시키는 방법이 있다. 숫자를 잘 선택하기 위한 전제조건은 숫자들이 정렬되어 있어야 하는데 무작위로 섞인 숫자들은 균형있게 선택하기가 어렵다.

균형을 맞추기 위해 트리를 회전한다.
트리를 회전시키기 위해서는 불균형의 원인이 되는 노드를 찾아야 한다.

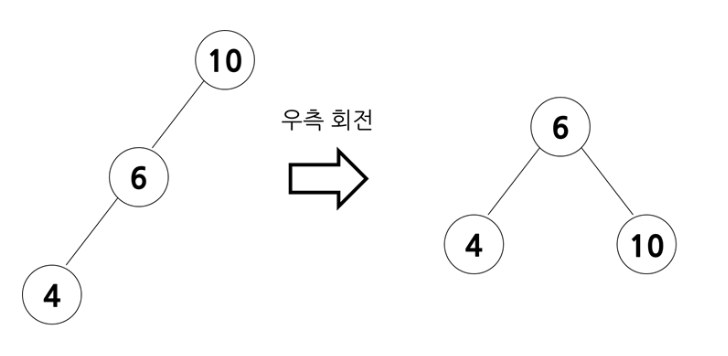
불균형이 왼쪽 서브트리에 나타나는 경우

우측 회전을 통해 조부모 노드를 부모 노드의 오른쪽 자식으로 옮겨 균형을 맞춘다.
- 4가 불균형의 원인이 되는 노드이며 4의 조부모 노드인 10을 오른쪽으로 회전 시켜 불균형을 해소하므로 우측 회전이라 한다.
- 회전이 완료되면 중간값이 트리의 중간에 가게 되어 다른 노드의 부모 역할을 한다.
크기 관계는 조부모 노드(grand parent) > 부모 노드(parent) > 자식 노드(child)

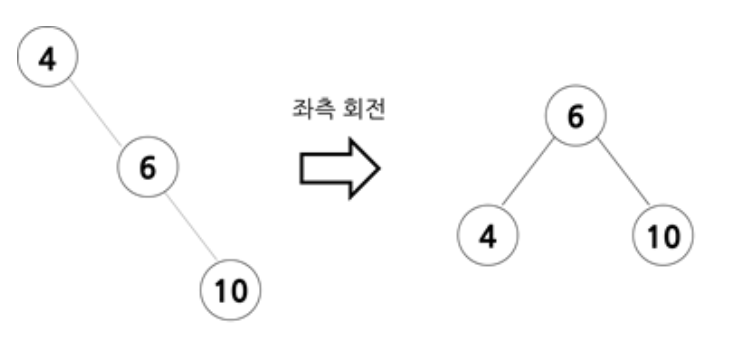
불균형이 오른쪽 서브트리에 나타나는 경우

좌측 회전을 통해 조부모 노드를 부모 노드의 왼쪽 자식으로 옮겨 균형을 맞춘다.
- 10이 불균형의 원인이 되는 노드이며 10의 조부모 노드를 왼쪽으로 회전 시켜 불균형을 해소하므로 좌측 회전이라 한다.
- 회전이 완료되면 중간값이 트리의 중간에 가게 되어 다른 노드의 부모 역할을 한다.
크기 관계는 조부모 노드(grand parent) < 부모 노드(parent) < 자식 노드(child)

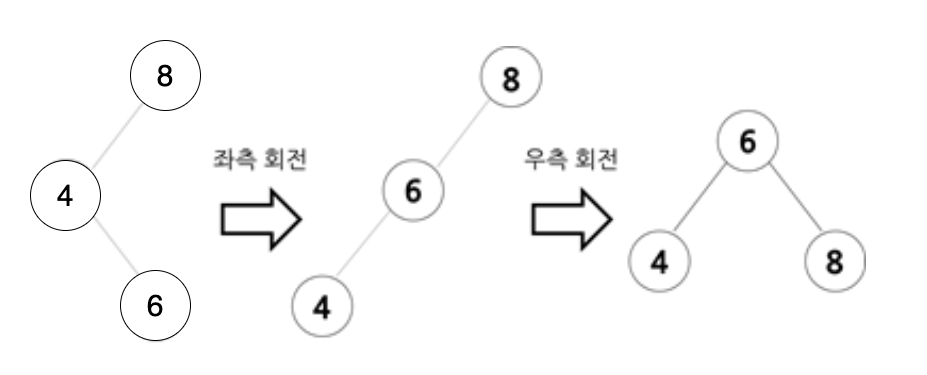
불균형이 오른쪽 자식의 왼쪽 서브트리에 나타나는 경우

우측 회전을 통해 중간값이 두 노드 사이에 위치하게 만들고 좌측 회전을 통해 불균형을 해소한다.
- 6을 중심으로 8을 우측 회전 시킨다.
- 8이 불균형의 원인이 되어 8의 조부모 노드인 4를 좌측 회전 시켜 불균형을 해소한다.
크기 관계는 부모 노드(parent) > 자식 노드(child) > 조부모 노드(grand parent)

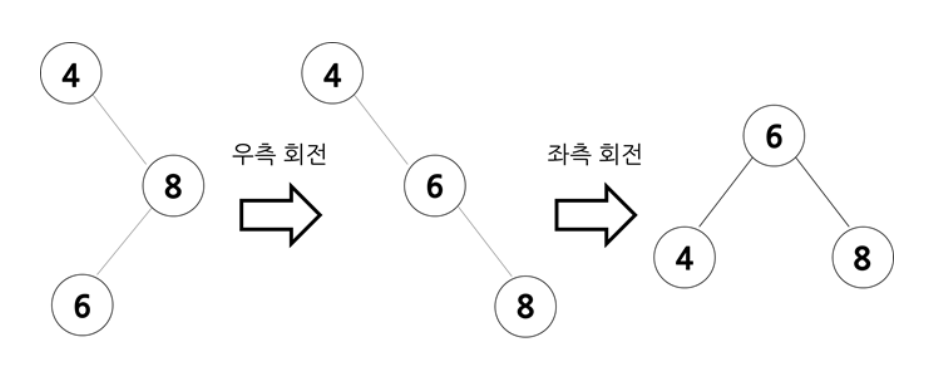
불균형이 왼쪽 자식의 오른쪽 서브트리에 나타나는 경우

좌측 회전을 통해 중간값이 두 노드 사이에 위치하게 만들고 우측 회전을 통해 불균형을 해소한다.
- 6을 중심으로 4를 좌측 회전 시킨다.
- 4가 불균형이 원인이 되어 4의 조부모 노드인 8을 우측 회전 시켜 불균형을 해소한다.
크기 관계는 부모 노드(parent) > 조부모 노드(grand parent) > 자식 노드(child)

	/**
	 * 주어진 노드를 기준으로 불균형한 트리를 좌측 회전하여 균형을 조정하는 메서드.
	 * @param node 불균형한 트리의 조부모 노드
	 * @return 균형이 조정된 트리의 새로운 루트 노드
	 */
	public Node<E> leftRotate(Node<E> node) {
		// 노드가 null 이거나 오른쪽 자식이 없으면 회전 불가능
		if (node == null || node.right == null) {
			return node;
		}

		Node<E> tmp = node.right; // 부모 노드
		node.right = tmp.left; // 부모 노드의 왼쪽 자식을 현재 노드의 오른쪽 자식으로 연결
		tmp.left = node; // 현재 노드를 부모 노드의 왼쪽 자식으로 연결

		return tmp; // 균형이 조정된 트리의 새로운 루트 노드 반환
	}

	/**
	 * 주어진 노드를 기준으로 불균형한 트리를 우측 회전하여 균형을 조정하는 메서드.
	 * @param node 불균형한 트리의 조부모 노드
	 * @return 균형이 조정된 트리의 새로운 루트 노드
	 */
	public Node<E> rightRotate(Node<E> node) {
		// 노드가 null 이거나 왼쪽 자식이 없으면 회전 불가능
		if (node == null || node.left == null) {
			return node;
		}

		Node<E> tmp = node.left; // 부모 노드
		node.left = tmp.right; // 부모 노드의 오른쪽 자식을 현재 노드의 왼쪽 자식으로 연결
		tmp.right = node; // 현재 노드를 부모 노드의 오른쪽 자식으로 연결

		return tmp; // 균형이 조정된 트리의 새로운 루트 노드 반환
	}

	/**
	 * 주어진 노드를 기준으로 불균형한 트리를 우측-좌측 회전하여 균형을 조정하는 메서드.
	 * @param node 불균형한 트리의 조부모 노드
	 * @return 균형이 조정된 트리의 새로운 루트 노드
	 */
	public Node<E> rightLeftRotate(Node<E> node) {
		// 노드가 null 이거나 오른쪽 자식이 없으면 회전 불가능
		if (node == null || node.right == null) {
			return node;
		}

		node.right = rightRotate(node.right); // 오른쪽 자식을 기준으로 우측 회전
		return leftRotate(node); // 왼쪽 회전 수행
	}

	/**
	 * 주어진 노드를 기준으로 불균형한 트리를 좌측-우측 회전하여 균형을 조정하는 메서드.
	 * @param node 불균형한 트리의 조부모 노드
	 * @return 균형이 조정된 트리의 새로운 루트 노드
	 */
	public Node<E> leftRightRotate(Node<E> node) {
		// 노드가 null 이거나 왼쪽 자식이 없으면 회전 불가능
		if (node == null || node.left == null) {
			return node;
		}

		node.left = leftRotate(node.left); // 왼쪽 자식을 기준으로 좌측 회전
		return rightRotate(node); // 우측 회전 수행
	}

📌 MyTree 구현

class Node<E> {
	E data; // 저장할 데이터
	Node<E> left; // 왼쪽 자식을 가리키는 포인터
	Node<E> right; // 오른쪽 자식을 가리키는 포인터

	public Node(E obj) {
		this.data = obj;
		left = right = null;
	}
}

public class Tree<E> {
	private Node<E> root;
	private int currentSize;

	public Tree() {
		this.root = null;
		currentSize = 0;
	}

	public Tree(Node<E> root) {
		this.root = root;
		currentSize = 1;
	}

	/**
	 * @param obj, 추가할 데이터
	 * @param node, 비교할 노드(root 부터 시작)
	 */
	@SuppressWarnings("unchecked")
	private void add(E obj, Node<E> node) {
		// 추가할 데이터가 현재 노드의 값보다 크면
		if (((Comparable<E>)obj).compareTo(node.data) > 0) {
			// 오른쪽으로 내려가야 한다.
			if (node.right == null) { // 오른쪽이 비어있으면 추가
				node.right = new Node<>(obj);
				return;
			}

			add(obj, node.right);
		}
		// 추가할 데이터가 현재 노드의 값보다 작거나 같으면
		// 왼쪽으로 내려가야 한다.
		if (node.left == null) {
			node.left = new Node<>(obj);
			return;
		}

		add(obj, node.left);
	}

	/**
	 * @param obj, 추가할 데이터
	 */

	public void add(E obj) {
		if (root == null) {
			root = new Node<>(obj);
		} else {
			add(obj, root);
		}
		currentSize++;
	}

	@SuppressWarnings("unchecked")
	private boolean contains(E obj, Node<E> node) {
		if (node == null) { // 트리 끝에 도달했
			return false;
		}

		if (((Comparable<E>)obj).compareTo(node.data) == 0) {
			return true;
		}

		if (((Comparable<E>)obj).compareTo(node.data) > 0) { // 찾으려는 값이 현재 노드보다 크면
			return contains(obj, node.right); // 오른쪽으로 이동
		} else { // 찾으려는 값이 현재 노드보다 작으면
			return contains(obj, node.left); // 왼쪽으로 이동
		}
	}

	public boolean contains(E obj) {
		return contains(obj, root);
	}

	/**
	 * 주어진 노드를 기준으로 불균형한 트리를 좌측 회전하여 균형을 조정하는 메서드.
	 * @param node 불균형한 트리의 조부모 노드
	 * @return 균형이 조정된 트리의 새로운 루트 노드
	 */
	public Node<E> leftRotate(Node<E> node) {
		// 노드가 null 이거나 오른쪽 자식이 없으면 회전 불가능
		if (node == null || node.right == null) {
			return node;
		}

		Node<E> tmp = node.right; // 부모 노드
		node.right = tmp.left; // 부모 노드의 왼쪽 자식을 현재 노드의 오른쪽 자식으로 연결
		tmp.left = node; // 현재 노드를 부모 노드의 왼쪽 자식으로 연결

		return tmp; // 균형이 조정된 트리의 새로운 루트 노드 반환
	}

	/**
	 * 주어진 노드를 기준으로 불균형한 트리를 우측 회전하여 균형을 조정하는 메서드.
	 * @param node 불균형한 트리의 조부모 노드
	 * @return 균형이 조정된 트리의 새로운 루트 노드
	 */
	public Node<E> rightRotate(Node<E> node) {
		// 노드가 null 이거나 왼쪽 자식이 없으면 회전 불가능
		if (node == null || node.left == null) {
			return node;
		}

		Node<E> tmp = node.left; // 부모 노드
		node.left = tmp.right; // 부모 노드의 오른쪽 자식을 현재 노드의 왼쪽 자식으로 연결
		tmp.right = node; // 현재 노드를 부모 노드의 오른쪽 자식으로 연결

		return tmp; // 균형이 조정된 트리의 새로운 루트 노드 반환
	}

	/**
	 * 주어진 노드를 기준으로 불균형한 트리를 우측-좌측 회전하여 균형을 조정하는 메서드.
	 * @param node 불균형한 트리의 조부모 노드
	 * @return 균형이 조정된 트리의 새로운 루트 노드
	 */
	public Node<E> rightLeftRotate(Node<E> node) {
		// 노드가 null 이거나 오른쪽 자식이 없으면 회전 불가능
		if (node == null || node.right == null) {
			return node;
		}

		node.right = rightRotate(node.right); // 오른쪽 자식을 기준으로 우측 회전
		return leftRotate(node); // 왼쪽 회전 수행
	}

	/**
	 * 주어진 노드를 기준으로 불균형한 트리를 좌측-우측 회전하여 균형을 조정하는 메서드.
	 * @param node 불균형한 트리의 조부모 노드
	 * @return 균형이 조정된 트리의 새로운 루트 노드
	 */
	public Node<E> leftRightRotate(Node<E> node) {
		// 노드가 null 이거나 왼쪽 자식이 없으면 회전 불가능
		if (node == null || node.left == null) {
			return node;
		}

		node.left = leftRotate(node.left); // 왼쪽 자식을 기준으로 좌측 회전
		return rightRotate(node); // 우측 회전 수행
	}

}

Twitter Facebook LinkedIn