6 분 소요

Reference

자바로 구현하고 배우는 자료구조


📌 What’s Heap?

  • 최대값 및 최소값을 찾아내는 연산을 빠르게 진행하기 위해 만들어진 완전 이진 트리(Complete Binary Tree)기반 자료구조

완전 이진 트리(Complete Binary Tree): 노드를 추가할 때 최하단 왼쪽 노드부터 차례대로 추가하는 트리

  • 왜 힙을 사용하나?
    • 배열의 경우 정렬되지 않았을 때 최대값과 최소값을 찾으려하면 최악의 경우 $O(N)$이 걸림
    • 힙에서는 최대값과 최소값을 찾으면, $O(log\ N)$이 걸림
    • 그래서 우선순위 큐처럼 최대값 또는 최소값을 빠르게 찾아야 하는 상황에 활용
  • 두 가지 종류가 존재
    • 최대 힙(Max Heap)
    • 최소 힙(Min Heap)

최대 힙(Max Heap)

  • 최대값을 구하기 위한 힙
    • 최대값이 root node에 존재
  • 규칙: 부모 노드가 자식 노드보다 크다
    • 부모 노드의 형제 노드들과 자식 노드는 상관 없다. 오직 자신의 자식 노드보다 크면 된다.
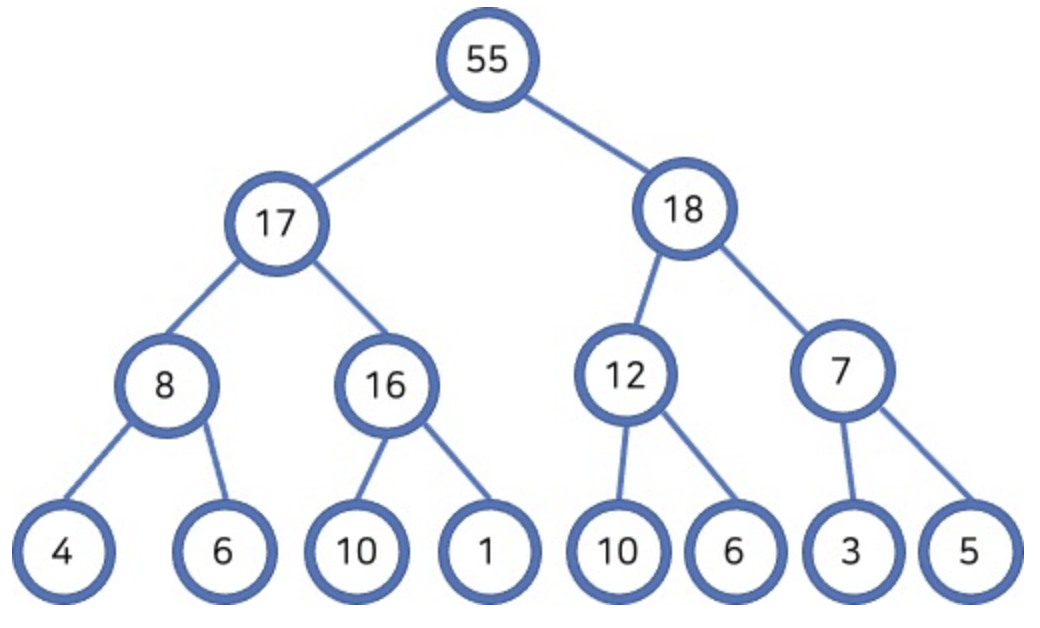
  • 트리에서의 높이(height): 루트에서부터 가장 먼 잎까지 가는데 거치게 되는 간선의 개수
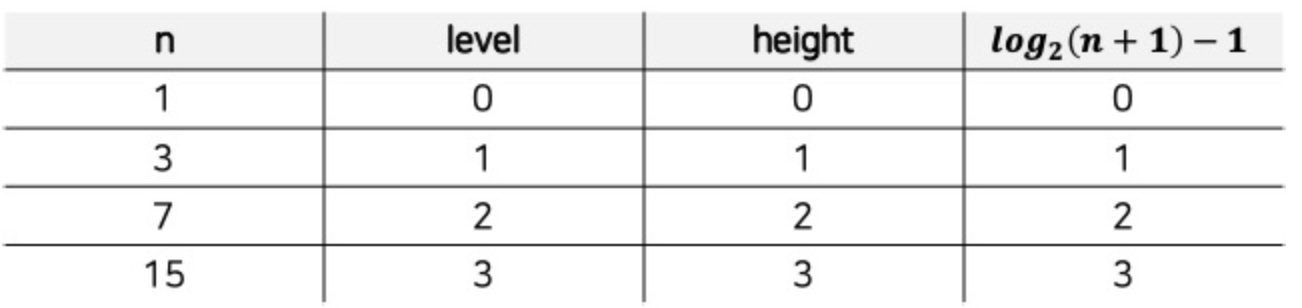
  • $log_2(n + 1) - 1$: 트리의 높이(height)와 일치
  • 즉, 트리에 존재하는 요소의 개수를 알면 트리의 높이를 계산할 수 있다

최소 힙(Min Heap)

  • 최소값을 구하기 위한 힙
    • 최소값이 root node에 존재
  • 규칙: 부모 노드가 자식 노드보다 작다
    • 부모 노드의 형제 노드들과 자식 노드는 상관 없다. 오직 자신의 자식 노드보다 작으면 된다.


📌 힙: 추가와 제거(Max Heap 기준)

추가

완전 이진 트리의 정의에 따라 최하단에 값을 추가하고 최대힙 규칙을 만족할때 까지 부모와 자식 노드를 교환한다.

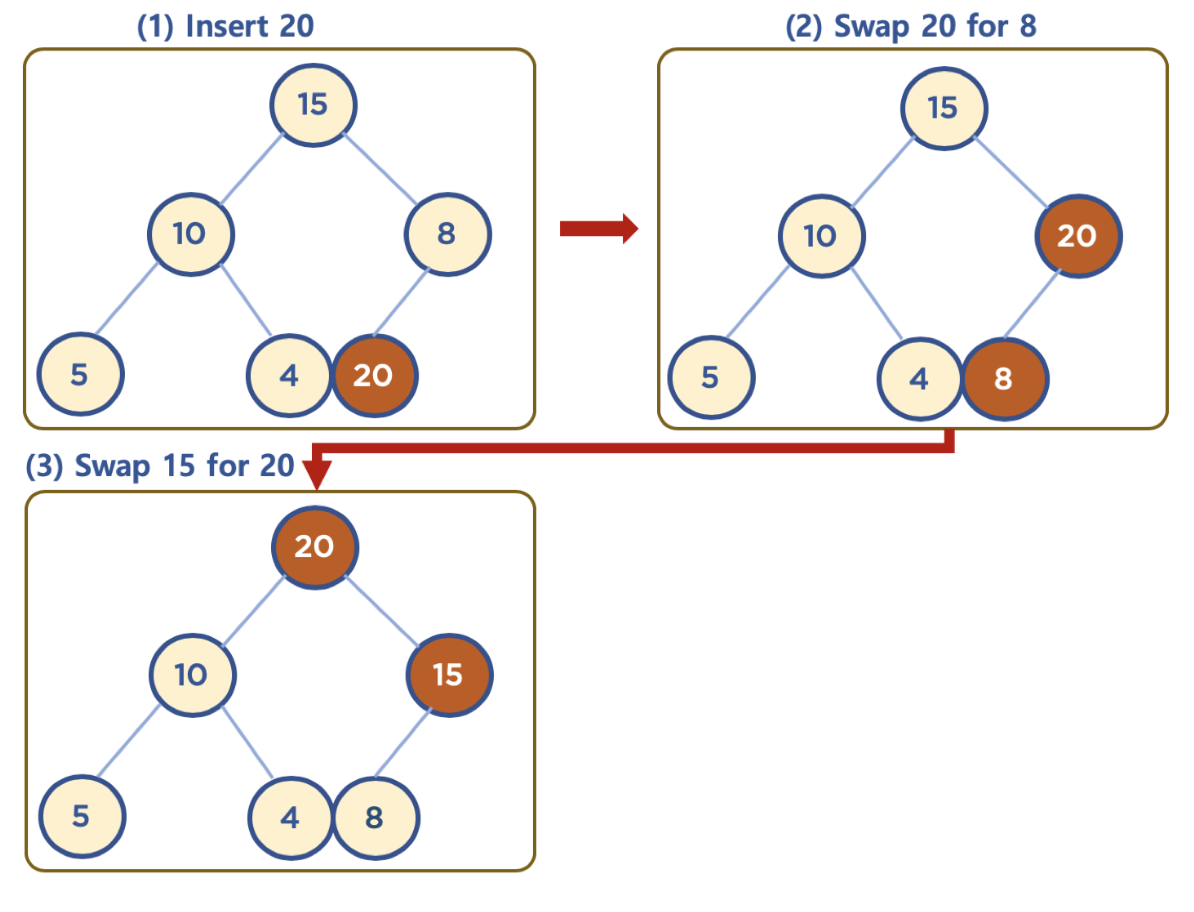
  • (1): 처음 20이라는 데이터를 힙에 추가하면 완전 이진 트리의 정의에 따라 비어있는 최하단 노드에 값을 추가한다
    • 최대힙 규칙 위반: 부모 노드인 8인 자식 노드인 20보다 작다
  • (2): 부모 노드와 자식 노드의 위치를 교환 (trickle up)
    • 최대힙 규칙 위반: 부모 노드인 15가 자식 노드인 20보다 작다
  • (3): 부모 노드와 자식 노드의 위치를 교환 (trickle up)
    • 최대힙 규칙 만족: 부모 노드인 20이 자식 노드인 10, 15보다 크다

제거

root node를 제거하고 마지막 요소를 root node로 이동시킨 뒤 최대힙 규칙을 만족할때 까지 부모와 자식 노드를 교환한다.

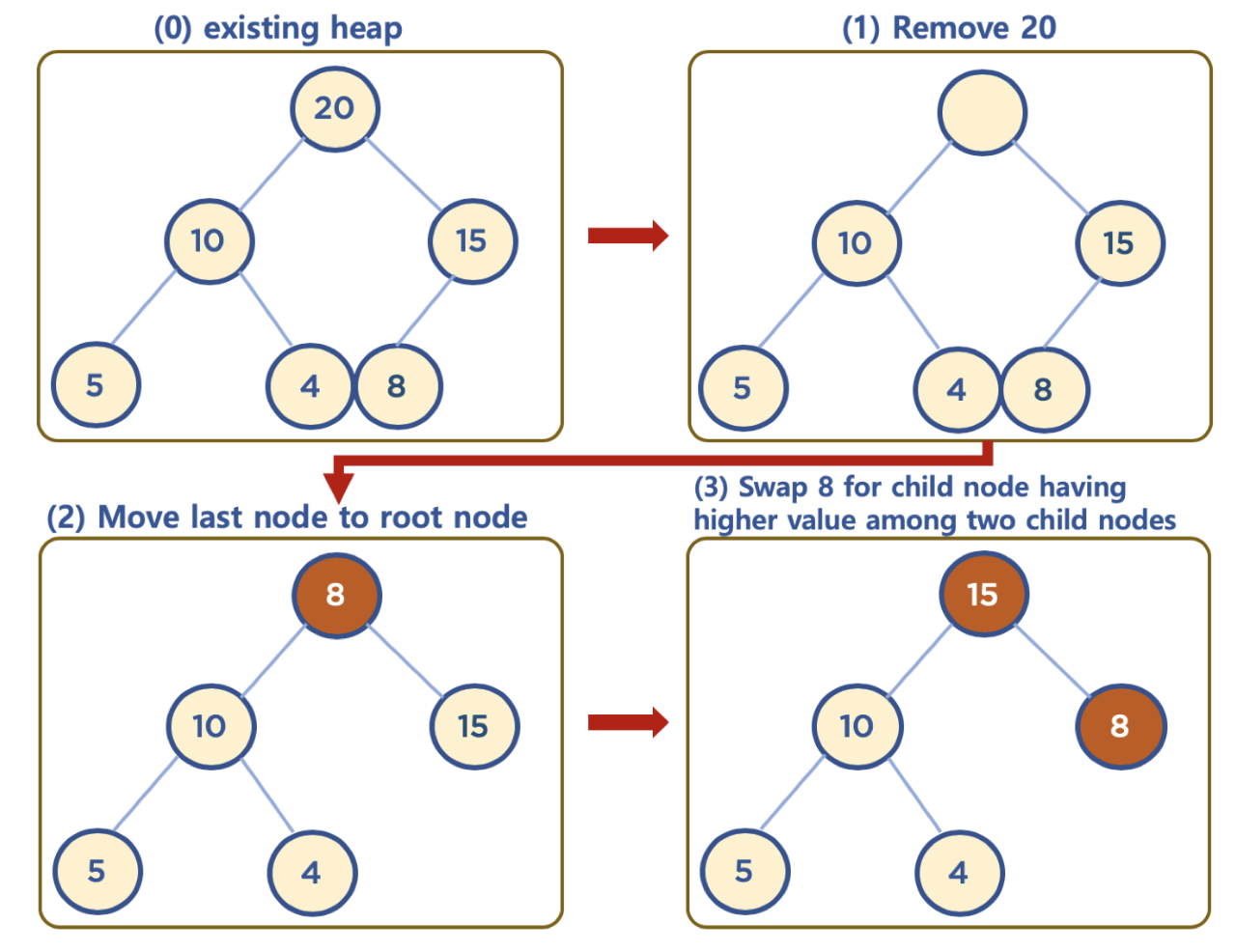
  • (1): 힙에서는 항상 root node를 제거, 20 제거
  • (2): 마지막 요소를 root node로 이동
    • 최대힙 규칙 위반: 부모 노드인 8이 자식 노드인 10, 15보다 작다
  • (3): 자식 노드 중 큰 값인 15와 자리를 교환 (trickle down)
    • 최대힙 규칙 만족: 부모 노드인 15가 자식 노드인 10, 8보다 크다


📌 Trickle Up: 추가

트리의 순회 방법 중 하나인 레벨 순서 순회를 이용한다. root node 부터 0, 1, 2, …, N 까지 번호를 부여한다.

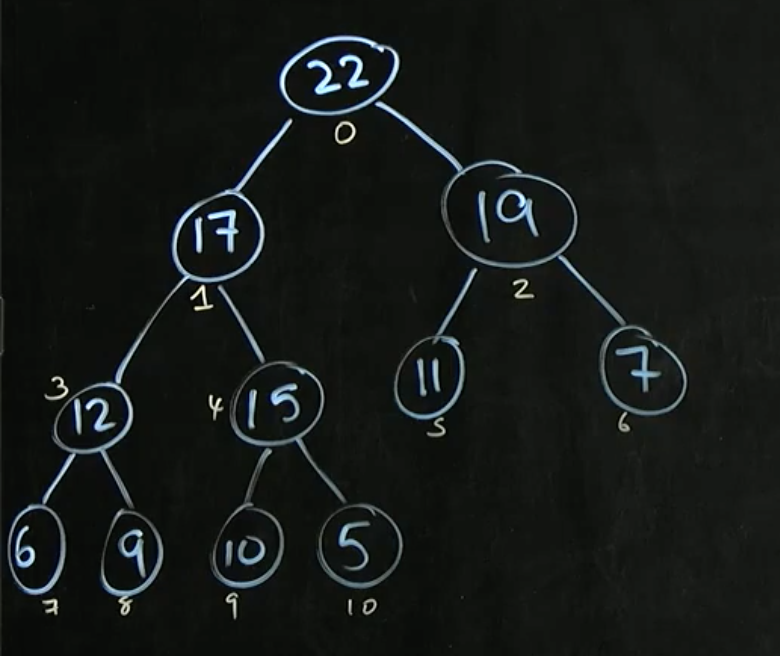
힙은 완전 이진 트리이기 때문에 자식 노드와 부모 노드 사이 일정한 성질을 갖는다.

  • 자식 노드 = $2 * parent + 1,\ 2 * parent + 2$
    • 3번 노드 12의 자식 노드는 = 7번 노드와 8번 노드 (2 * 3 + 1, 2 * 3 + 2)
  • 부모 노드 = $floor({ {child - 1}\over{2} })$
    • floor: 소수점 이하 버림
public class Heap<E> {
	private static final int DEFAULT_SIZE = 10;

	private int lastPosition; // 힙이 시작점에서 얼마나 떨어져 있는지 나타냄, 어디까지 요소를 넣었는지 기록
	private final E[] array;

	public Heap() {
		this.array = (E[])new Object[DEFAULT_SIZE];
	}

	/**
	 * 마지막 위치에 요소를 추가하고 Trickle Up을 통해 힙 규칙을 만족시킨다.
	 * @param object, 추가할 요소
	 */
	public void add(E object) {
		array[++lastPosition] = object; // 마지막 위치 다음에 요소를 추가
		trickleUp(lastPosition);
	}

	public void swap(int from, int to) {
		E tmp = array[from];
		array[from] = array[to];
		array[to] = tmp;
	}

	/**
	 * root 까지 도달하면 early return
	 * 부모 노드와 비교해 크다면 swap 후 힙 규칙을 만족할 때 까지 Trickle Up
	 * @param position, 요소의 현재 위치
	 */
	public void trickleUp(int position) {
		if (position == 0) {
			return;
		}

		int parent = (int)Math.floor((position - 1) / 2);
		if (((Comparable<E>)array[position]).compareTo(array[parent]) > 0) {
			swap(position, parent);
			trickleUp(parent);
		}
	}

}


📌 Trickle Down: 제거

	/**
	 * 힙은 root node 만 제거할 수 있음
	 * 마지막 노드와 루트 노드를 바꾼 후 lastPosition 값을 줄여 배열에 없는 값으로 취급
	 * 최대 힙 규칙을 만족할 때 까지 Trickle Down
	 * @return root node
	 */
	public E remove() {
		E tmp = array[0];
		swap(0, lastPosition--);
		trickleDown(0);
		return tmp;
	}

	public void trickleDown(int parent) {
		int left = 2 * parent + 1;
		int right = 2 * parent + 2;

		// 마지막 위치가 왼쪽 자식이고, 자식이 부모보다 클 때
		if (left == lastPosition && (((Comparable<E>)array[parent]).compareTo(array[left])) < 0) {
			swap(parent, left);
			return;
		}

		// 마지막 위치가 오른쪽 자식이고, 자식이 부모보다 클 때
		if (right == lastPosition && (((Comparable<E>)array[parent]).compareTo(array[right])) < 0) {
			swap(parent, right);
			return;
		}

		// 계산한 자식들의 위치가 lastPosition 보다 크거나 같으면 종료 (끝까지 도착함)
		if (left >= lastPosition || right >= lastPosition) {
			return;
		}

		if ( // 왼쪽 자식이 오른쪽 자식보다 더 크고, 왼쪽 자식이 부모보다 클 때
			(((Comparable<E>)array[left]).compareTo(array[right])) >= 0
				&& (((Comparable<E>)array[left]).compareTo(array[parent])) > 0
		) {
			swap(parent, left);
			trickleDown(left);
		} else if ( // 오른쪽 자식이 왼쪽 자식보다 더 크고, 오른쪽 자식이 부모보다 클 때
			(((Comparable<E>)array[right]).compareTo(array[parent])) > 0
		) {
			swap(parent, right);
			trickleDown(right);
		}

	}

📌 힙의 정렬(Heap Sort)

힙에서 요소를 제거할 때 root node를 제거하고 마지막 요소와 자리를 바꾼 후 trickleDown()을 진행하고, lastPosition을 줄여 마지막 위치로 간 root node는 힙의 일부로 생각하지 않는다.

  • 처음 상태
  • remove(): root node와 마지막 요소인 5가 자리를 바꾼 후 22는 힙에서 제외
  • 힙 규칙을 만족하기 위해 trickleDown()진행
  • 다시 remove()
  • 힙 규칙을 만족하기 위해 trickleDown()진행
  • 위 과정을 계속 반복하면 요소가 오름차순으로 정렬된다.

힙 정렬 알고리즘

  • 요소를 계속 제거하면서 자동으로 정렬된다.
  • $O(N\ logN)$의 시간복잡도를 가진다.
    • 두 수를 비교해서 하나를 고르는 방식으로 숫자를 골라내기 때문
    • 총 N개의 숫자를 $logN$개의 숫자와 비교
  • 데이터의 복사본을 만들 필요없이 순서를 바꿔 정렬하기 때문에 공간 복잡도가 낮다.


📌 MyIntegerHeap 구현

import java.util.Arrays;

public class IntegerHeap<Integer> {

	private static final int DEFAULT_SIZE = 10;

	private int lastPosition; // 힙이 시작점에서 얼마나 떨어져 있는지 나타냄, 어디까지 요소를 넣었는지 기록
	private final int[] array;

	public IntegerHeap() {
		this.array = new int[DEFAULT_SIZE];
		lastPosition = 0;
	}

	public IntegerHeap(int size) {
		this.array = new int[size];
		lastPosition = 0;
	}

	/**
	 * 마지막 위치에 요소를 추가하고 Trickle Up을 통해 힙 규칙을 만족시킨다.
	 * @param object, 추가할 요소
	 */
	public void add(int object) {
		array[++lastPosition] = object; // 마지막 위치 다음에 요소를 추가
		trickleUp(lastPosition);
	}

	public void swap(int from, int to) {
		int tmp = array[from];
		array[from] = array[to];
		array[to] = tmp;
	}

	/**
	 * root 까지 도달하면 early return
	 * 부모 노드와 비교해 크다면 swap 후 힙 규칙을 만족할 때 까지 Trickle Up
	 * @param position, 요소의 현재 위치
	 */
	public void trickleUp(int position) {
		if (position == 0) {
			return;
		}

		int parent = (int)Math.floor((position - 1) / 2);
		if (array[position] > array[parent]) {
			swap(position, parent);
			trickleUp(parent);
		}
	}

	/**
	 * 힙은 root node 만 제거할 수 있음
	 * 마지막 노드와 루트 노드를 바꾼 후 lastPosition 값을 줄여 배열에 없는 값으로 취급
	 * 최대 힙 규칙을 만족할 때 까지 Trickle Down
	 * @return root node
	 */
	public int remove() {
		int tmp = array[0];
		swap(0, lastPosition--);
		trickleDown(0);
		return tmp;
	}

	@Override
	public String toString() {
		return "Heap{" +
			"array=" + Arrays.toString(array) +
			'}';
	}

	public void trickleDown(int parent) {
		int left = 2 * parent + 1;
		int right = 2 * parent + 2;

		// 마지막 위치가 왼쪽 자식이고, 자식이 부모보다 클 때
		if (left == lastPosition && array[left] > array[parent]) {
			swap(parent, left);
			return;
		}

		// 마지막 위치가 오른쪽 자식이고, 자식이 부모보다 클 때
		if (right == lastPosition && array[right] > array[parent]) {
			swap(parent, right);
			return;
		}

		// 계산한 자식들의 위치가 lastPosition 보다 크거나 같으면 종료 (끝까지 도착함)
		if (left >= lastPosition || right >= lastPosition) {
			return;
		}

		// 왼쪽 자식이 오른쪽 자식보다 더 크고, 왼쪽 자식이 부모보다 클 때
		if (array[left] > array[right] && array[left] > array[parent]) {
			swap(parent, left);
			trickleDown(left);
		} else if ( // 오른쪽 자식이 왼쪽 자식보다 더 크고, 오른쪽 자식이 부모보다 클 때
			array[right] > array[parent]
		) {
			swap(parent, right);
			trickleDown(right);
		}

	}
}

class Main {
	public static void main(String[] args) {
		IntegerHeap<Integer> heap = new IntegerHeap<>(12);

		heap.add(22);
		heap.add(17);
		heap.add(19);
		heap.add(12);
		heap.add(15);
		heap.add(11);
		heap.add(7);
		heap.add(6);
		heap.add(9);
		heap.add(10);
		heap.add(5);

		System.out.println(heap);
		// Heap{array=[22, 19, 17, 7, 12, 15, 11, 0, 6, 9, 10, 5]}
		for (int i = 0; i < 11; i++) {
			heap.remove();
		}

		System.out.println(heap);
		// Heap{array=[0, 6, 5, 7, 9, 10, 11, 12, 15, 17, 19, 22]}
	}
}

댓글남기기

참고

[프로그래밍] 좋은 테스트 코드 작성하기

6 분 소요

References Testing, Oh my! 스프링 캠프 2019: 무엇을 테스트할 것인가? 어떻게 테스트할 것인가? [번역글] UnitTest By Martin Fowler 3월 우아한테크세미나: 우아한 ATDD

[자바] final 키워드 & 불변 객체

2 분 소요

References [10분 테코톡]시카의 Java final과 불변 객체) 불변 객체(Immutable Object) 및 final을 사용해야 하는 이유 - Mangkyu님 블로그

[자바] Java Enum

2 분 소요

References Java Enum 활용기 - 우아한 기술 블로그